Co to jest rezystancja i rezystywność? Czym jest przewodność i konduktancja? Co wpływa na rezystancję? Które materiały są najlepszymi przewodnikami?
Jeśli jeszcze nie wiesz czym jest prąd elektryczny i co jest niezbędne do jego powstania, to koniecznie przejrzyj artykuł poniżej:
Dziś ta wiedza nam się przyda, gdyż skupimy się na utrudnieniach jakie napotkać na swej drodze może prąd elektryczny. Zapraszam na artykuł poświęcony rezystancji!
Prąd i siła
Mówi się, że nie ma prądu bez napięcia. Napięcie elektryczne traktowane jest jak siła tłocząca ładunki wewnątrz przewodów elektrycznych. Nie bez powodu w wielu książkach napięcie porównuje się do ciśnienia w instalacji wodnej, jednak według mnie nie jest to do końca prawdą. Nie ma wszak mowy o ruchu bez siły, a napięcie siłą nie jest. Napięcie określa jedynie jak dużo energii ładunki nam dostarczą, a tym co naprawdę wprawia je w ruch jest siła Coulomba.
Czy wiesz co tak naprawdę robią wszystkie znane nam w fizyce siły? Przyspieszają obiekty. Cięższe ciała przyspieszają wolniej, lżejsze szybciej, ale dopóki nic nie stanie im na drodze to będą one przyspieszane bez końca. Zasadzie tej podlega każdy, nawet najlżejszy obiekt i obrazuje ją poniższe, niezwykle proste równanie:
F = m · a
Choć ładunki elektryczne są niezwykle małe to i one podlegają zasadom dynamiki. W trakcie przepływu prądu, siła Coulomba nieustannie je przyspiesza, a więc ich prędkość cały czas rośnie. Natężenie prądu (I) wyrażamy poprzez ilość ładunku (Q) przepływającego w każdej sekundzie (t). Skoro ładunki nieustannie przyspieszają, to natężenie prądu również powinno z czasem rosnąć!
I = Q / t
A jednak… tak się w rzeczywistości nie dzieje. Przez zwykłą żarówkę o mocy 100 W, podłączoną do napięcia 230 V popłynie prąd o natężeniu około 0,5 ampera. Wartość ta będzie taka sama po pierwszej, piątej, czy nawet dziesiątej godzinie pracy. Dlaczego tak się dzieje? Czyżby ładunki nie były przez cały czas przyspieszane? Czy coś stoi im na drodze?
Ładunki elektryczne nie mają lekko
Przepływ prądu elektrycznego podobny jest do próby przejazdu przez centrum miasta w dzień roboczy po godzinie 14:00. Wyjeżdżamy z pracy, przyspieszamy, czerwone światło, korek i stoimy. Zapala się zielone, przyspieszamy, kolejny korek, stoimy. Struktura metalowego przewodnika (na przykład miedzi), to istne skupisko czerwonych świateł. Każdy wolny elektron biorący udział w zbiorowym przepływie przyspieszany jest przez siłę Coulomba, po czym wpada z impetem na jeden z atomów metalu i niemal całkowicie wytraca prędkość. Gęstość materiału sprawia, że tryliony małych elektronów nie są w stanie nawet porządnie się rozpędzić pomiędzy kolejnymi zderzeniami, a zjawisko prądu elektrycznego przypomina prawdziwy chaos.
Powyższa animacja przedstawia teorię przepływu ładunku opracowaną około 150 lat temu i trochę się od tego czasu pozmieniało. Głównie dzięki mechanice kwantowej wiemy, że przepływ ładunku elektrycznego jest znacznie bardziej skomplikowany i zagadkowy niż przypuszczaliśmy. Ale czy to znaczy, że powyższa wizja wesoło odbijających się niebieskich kuleczek jest błędna? Ależ skąd! Jest ona tylko… nieco uproszczona. I w niczym to nie przeszkadza, gdyż takie właśnie wyobrażenie oparte w 100% na mechanice klasycznej było podstawą odkrycia i opisania zjawiska nazwanego rezystancją.
Czym jest rezystywność i konduktancja?
Natężenie prądu opisuje tempo przepływu ładunków, a napięcie ich energię. Rezystancja utrudnia życie obu tym wielkościom – z powodu kolizji ładunki tracą energię i znacząco zwalniają. Innymi słowy rezystancja wyraża opór jaki materiał stawia zjawiskom elektrycznym. Warto w takim razie zastanowić się od czego zależy wielkość tego ,,oporu” i które materiały mają największa, a które najmniejszą rezystancję.
Teoria mówi, że wszystkie przewodniki (np. metale) przewodzą prąd, a izolatory (np. guma, szkło) prądu nie przewodzą. Rzeczywistość nie jest jednak tak czarno-biała, a materiał materiałowi nie równy. O tym, że nie ma izolatorów idealnych powiemy sobie innym razem, przy okazji omawiania napięcia przebicia. Zjawisko rezystancji interesować nas będzie głównie tam, gdzie prąd może płynąć dość wartkim strumieniem – w przewodnikach. Czym zatem różnią się od siebie poszczególne materiały i co wpływa na ich opór?

Najistotniejszym czynnikiem w kwestii rezystancji jest sama budowa przewodników. Atomy z których są one zbudowane mają różne rozmiary, są inaczej ,,upakowane” i każdy z nich charakteryzuje inna liczba wolnych elektronów biorących udział w przepływie. Żeby się w tych wszystkich własnościach nie zagubić zebrano jest pod wspólną nazwą oporu właściwego, zwanego fachowo rezystywnością. Aby obliczyć rezystywność wybranego materiału, musielibyśmy znać cały szereg jego cech wraz z temperaturą samego przewodnika!. Na szczęście inni fizycy już się tym wcześniej zajęli i powstały tabele, z których wartość rezystywności możemy bez problemu odczytać:
Rezystywność wybranych materiałów (20°C)
| Materiał | Rezystywność [Ω·m] | Materiał | Rezystywność [Ω·m] |
|---|---|---|---|
| Srebro | 1,59 · 10-8 | Woda morska | 2,00 · 10-1 |
| Miedź | 1,68 · 10-8 | German | 4,60 · 10-1 |
| Złoto | 2,44 · 10-8 | Woda pitna | 2,00 · 101 |
| Aluminium | 2,82 · 10-8 | Krzem | 6,40 · 102 |
| Wapń | 3,36 · 10-8 | Drewno (wilgotne) | 1,00 · 103 |
| Wolfram | 5,60 · 10-8 | Woda ultra-czysta | 1,80 · 105 |
| Cynk | 5,90 · 10-8 | Szkło | 1,00 · 1011 |
| Żelazo | 1,00 · 10-7 | Diament | 1,00 · 1012 |
| Platyna | 1,06 · 10-7 | Twarda guma | 1,00 · 1013 |
| Cyna | 1,09 · 10-7 | Drewno (suche) | 1,00 · 1014 |
| Ołów | 2,20 · 10-7 | Siarka | 1,00 · 1015 |
| Tytan | 4,20 · 10-7 | Powietrze | 3,30 · 1016 |
| Stal nierdzewna | 6,90 · 10-7 | Parafina | 1,00 · 1017 |
| Rtęć | 9,80 · 10-7| Szkło kwarcowe | 7,50 · 1017 | |
| Chromonikielina | 1,10 · 10-6 | Teflon | 1,00 · 1025 |
Im niższa rezystywność, tym łatwiej ładunkom przedrzeć się przez materiał. Pod tym względem królem wśród przewodników jest bez wątpienia srebro. Niestety z uwagi na jego wysoką cenę, przewody elektryczne wytwarza się z nieco tylko gorszej miedzi, a w elektronice, gdzie niezbędna jest wysoka odporność na korozję, stosuje się złoto. Jeśli widzisz te liczby i za bardzo one do ciebie nie przemawiają, to mam na to radę. Już dawno temu ktoś wpadł na pomysł, by zamiast męczyć się z niewielkimi wartościami rezystywności metali mówić o tym jak świetnie potrafią przewodzić. W ten sposób liczby bardzo małe można zamienić na duże, a wszystko to dzięki wielkości zwanej konduktywnością lub po prostu przewodnictwem elektrycznym właściwym. Konduktywność (symbol γ) jest w rzeczywistości odwrotnością rezystywności (symbol ρ) – mówi o tym jak łatwo jest ładunkom przenikać strukturę materiału. Matematycznie zapisać możemy to w ten sposób:
γ = 1 / ρ
Na przykład konduktywność srebra wynosi 61,9 · 106 S/m, a miedzi 58,5 · 106 S/m. Jak widać liczby stały się naprawdę duże, a na dodatek jednostką konduktywności jest przedziwny simens na metr [S/m]. Fakt, rezystywność wyrażana w omometrach [Ω·m] to też nie jest coś intuicyjnego, ale o omach każdy młody elektryk kiedyś już słyszał, a o simensach niekoniecznie. Stąd przez resztę artykułu pozostaniemy jednak przy znacznie popularniejszych omach, za co mam nadzieję Werner Siemens się nie obrazi.
Czym jest rezystancja?
Bardzo fajnie porównuje się oporności właściwe różnych metali w tabeli, ale rezystywność to nie rezystancja i do pełnego obrazka musimy wziąć pod uwagę jeszcze kilka czynników. Jak myślisz, czy elektronom łatwiej jest zasilić urządzenie oddalone o 2 metry, czy o 100 kilometrów? Albo dlaczego przewody elektryczne są tak grube i nie staramy się oszczędzić tysięcy ton miedzi przesyłając energię cieniutkimi, miedzianymi żyłkami?
Odpowiedzią na oba pytania jest fakt, że długość i przekrój przewodnika mają istotny wpływ na opór stawiany ładunkom. Sprawdźmy to na dwóch prostych przykładach.
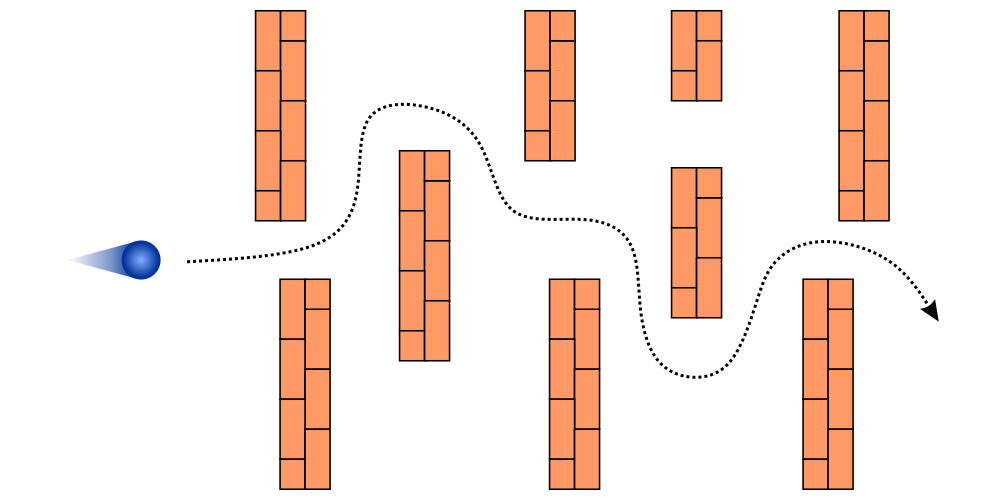
Przykład 1 – Długość przewodnika
Załóżmy, że pewien elektron pod wpływem siły kulomba porusza się w przewodzie, lecz na drodze stoją przeszkody w postaci 5 atomów przewodnika (przykład a na obrazku). Zderzając się z nimi, elektron traci prędkość i rozprasza zdobytą energię kinetyczną. Ostatecznie do mety dociera on po około sekundzie.

W drugim scenariuszu (przykład b z obrazka) ten sam elektron do pokonania ma dwukrotnie dłuższy przewodnik, co oznacza dwa razy więcej przeszkód na drodze. W rezultacie cząsteczka osiąga linie mety dopiero po dwóch sekundach, rozpraszając dwukrotnie więcej cennej energii. Wynika z tego, że im dłuższy przewodnik, tym więcej zderzeń i tym większa jest rezystancja.
Przykład 2 – Grubość przewodnika
Przypuśćmy, że nasz przewód ma taką grubość, iż tylko dwa elektrony mogą płynąć jednocześnie obok siebie (przykład a z obrazka poniżej). W trakcie ruchu oba elektrony dokonują tej samej ilości zderzeń i na metę wpadają po czasie równym 1 s. Bilans zderzeń wynosi 5 na każdy elektron, przy dwóch cząsteczkach na mecie
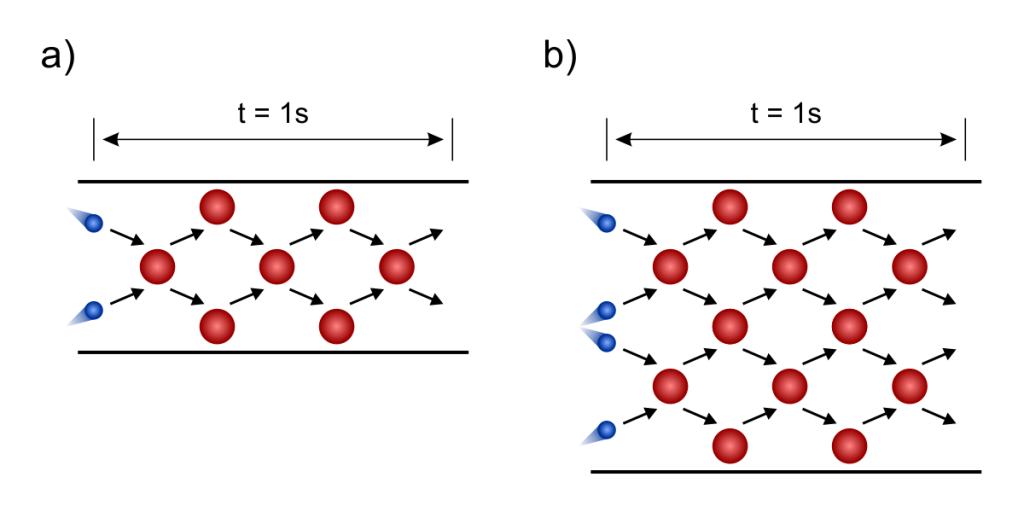
Przypadek numer dwa to przewód dwukrotnie grubszy, dzięki czemu obok siebie mogą płynąć jednocześnie aż cztery cząsteczki. Długość przewodnika się nie zmieniła, a więc wszystkie wpadają na metę po około sekundzie. W tym wypadku bilans zderzeń to ponownie 5 na każdy elektron, ale tutaj w tym samym czasie na metę dotarły aż 4 cząsteczki. Więcej elektronów to oczywiście większy prąd i więcej dostarczonej energii. Zasada jest zatem jasna: im grubszy przewód, tym mniejsza jest jego rezystancja.
Definicja rezystancji
To już wszystkie elementy układanki jakich potrzebujemy. Wiemy, że rezystancja zależy od oporu właściwego przewodnika (symbol ρ) oraz od jego długości (l) i przekroju (A). Całość zamknąć możemy w prostym i eleganckim równaniu:
![]()
Symbolem rezystancji jest duża litera R, a jej jednostką został om (symbol Ω). Dzięki powyższemu równaniu bez problemu policzysz, że dwużyłowy, miedziany przewód o przekroju 1,5 mm2 i długości 10 m ma rezystancję równą 0,112 Ω. Czy taka wartość to duża rezystancja? Jaki wpływ ma ona na prąd i napięcie przy zasileniu małej żarówki albo dużego silnika elektrycznego? Jaką moc jesteśmy w stanie takim przewodem dostarczyć? Czy może stać się z nim coś złego, jeśli prąd będzie zbyt duży?
Na te pytania nie jestem dziś w stanie ci odpowiedzieć. Jeśli jednak zajrzysz tutaj za jakiś czas, to w kolejnych artykułach poznasz więcej istotnych i na pewno zaskakujących faktów na temat rezystancji. Do zobaczenia!
Bibliografia
- Podstawy teorii pola elektromagnetycznego – Z. Piątek, P. Jabłoński, Wydawnictwo Naukowo-Techniczne,
- Podstawy Elektrodynamiki – D. Griffiths, Wydawnictwo Naukowe PWN,
- Fizyka ciała stałego – N. Ashcroft, N. Mermin, Wydawnictwo Naukowo-Techniczne,
- Podstawy Elektrotechniki, zagadnienia wybrane – S. Krakowiak, Warszawa,
- Metaloznawstwo, praca zbiorowa – Politechnika Gdańska, Gdańsk







Nadal nie rozumiem, jak rezystor ogranicza pobór prądu. Na przykład dając rezystor szeregowo z diodą LED zabezpiecza on diodę przed spaleniem, natomiast gdyby tego rezystora nie było to dioda się spali. Podobnie gdyby zewrzeć dwa bieguny baterii kablem. Kabel się spali. Rozumiem, że rezystor ma ograniczać prąd, ale co to da, jeśli np. dioda LED połączona do baterii z założenia bierze nieskończenie wiele prądu dopóki się nie spali. To jeśli dołożymy rezystor to początkowa wartość prądu będzie mniejsza, ale nadal będzie rosła. Jednak tak jak opisano początkowo w artykule na przykładzie żarówki tak nie jest. Wiem, że moje rozumowanie jest gdzieś błędne, dlatego jestem ciekaw odpowiedzi.
Napisałeś: ,,To jeśli dołożymy rezystor to początkowa wartość prądu będzie mniejsza, ale nadal będzie rosła”. Dlaczego będzie rosła? Co miałoby powodować ten wzrost?
Przez to, że jest dioda LED w obwodzie, która chce tego prądu nieskończenie wiele. Dołożenie rezystora rozumiem jako takie ograniczenie, przez które zamiast pobór prądu startować z 2A obwód zacznie pobór od 1A, dzięki rezystorowi, ale pobór nadal będzie rósł w nieskończoność przez diodę LED. Nie rozumiem, czemu np. żarówka nie potrzebuje rezystora lub po prostu czemu pewne elementy nie biorą nieskończenie wiele prądu(np. żarówka) ale już sam kabel między biegunami tak i powoduje zwarcie.
Ok, już wyjaśniam:
1. Uściślę, że dioda LED nie pobiera nieskończenie wiele prądu. Podłącz diodę do napięcia 3 V, a zobaczysz, że nie pobierze ona więcej niż kilka miliamperów. Zgodzę się jednak, że dioda LED może pobrać baaardzo duży prąd (co wynika z jej niewielkiej rezystancji). Jak więc dodatkowy rezystor ogranicza ten prąd? Odpowiedź w punkcie 2.
2. Wyobraź sobie gruby wąż ogrodowy – to nasz obwód. Na końcu węża jest jakaś końcówka ogrodowa – to nasza dioda. Nie może ona oczywiście wyrzucić z siebie nieskończenie dużo wody, ale załóżmy, że całkiem spory strumień może z niej polecieć. A teraz ten długi wąż w jednym miejscu zaginamy, czyli dodajemy rezystancję. Co się dzieje? Z końcówki węża leci teraz bardzo mało wody. Końcówka (dioda) jest cały czas ta sama, a więc cały czas jest ona w stanie wyrzucić tyle samo wody. Ale co z tego, skoro tej wody po prostu nie ma? To jest właśnie rola rezystancji. Hamuje ona prąd tak, by zbyt dużo nie popłynęło go przez diodę. Po co się to robi? Bo duży prąd to dużo ciepła, a przez to dioda może się bez trudu spalić.
3. Dlaczego zwykła żarówka nie potrzebuje rezystora? Bo ona jest jakby ,,dwa w jednym”. Jej żarnik jest jednocześnie rezystorem i źródłem światła. Diody LED to niemal czyste źródła światła, więc w ich przypadku trzeba trochę więcej pokombinować (np. dołożyć rezystor, albo dobrać odpowiednio niskie napięcie).
4. Dlaczego przewód między biegunami powoduje zwarcie? Bo jego rezystancja jest nawet niższa niż diody LED i może on przepuścić jeszcze więcej prądu.
Najlepszym zobrazowaniem przepływu prądu elektrycznego jest kołyska/wahadło Niutona, czyli ciasno zawieszone kuleczki/wahadła odbijające jedno drugą. Też model mechaniczny.
Jak długo będziemy jeszcze wprowadzani w błąd przez teorie „płynie prąd” i o oporze jako przeszkoda dla płynącego prądu z sprzed 150lat?
Elektron porusza się (dryf) z szybkością 1/10mm /sekundę .Przykładowo, elektron opuszczając źródło np. baterie oddaloną o 100 metrów dotrze do nas po 28 godzinach. Żaden więc elektron z baterii nie dopłynie do żarówki aby pod wpływem oporu tarcia rozgrzać jej włókno aby świeciła. Skąd pomysł, ze elektrony wypychane /wypompowane są, ze źródła np baterii, lecą/płyną po kablach /przewodach, potykają ,odbijają się, zderzają z atomami, przez co rozpraszają swoją energie???
Z budowy atomu wiadome jest że liczba protonów jest równa liczbie elektronów. Elektrony krążą wokół jądra na różnych orbitach. Elektron znajdujący się na ostatniej, najbardziej zewnętrznej powłoce atomu( tzw powłoka walencyjna ) jest najmniej związany ” siłowo” z jądrem, i istnieje zdelokalizowanie- to znaczy tworzące je elektrony są uwspólniane przez więcej niż dwa atomy. Pod wpływem przyłożonego napięcia elektrycznego, w metalach elektrony walencyjne mogą się przemieszczać między węzłami sieci krystalicznej, w całej jego objętości dzięki czemu oraz tworzących się i powstających pasma zdelokalizowanych elektronów, są dobrymi przewodnikami elektrycznymi i z tego względu nazwane zostały one elektronami swobodnymi. Gdzie tu jest opór, przeszkody i inne przedstawiane w prezentacji graficznej z piłeczkami???
,,Jak długo będziemy jeszcze wprowadzani w błąd przez teorie „płynie prąd” i o oporze jako przeszkoda dla płynącego prądu z sprzed 150lat?”
Myślę, że jeszcze dość długo będziemy tak robić, bo jest to doskonałe uproszczenie, które pozwala ludziom na zrozumienie i zapamiętanie podstawowych idei elektrotechnicznych bez potrzeby zagłębiania się w mechanizmy fizyczne.
,,Elektrony krążą wokół jądra na różnych orbitach.” – dlaczego krytykujesz moje 150-letnie rozważania, samemu przedstawiając budowę atomu z tamtego okresu? Wiemy obecnie, że wcale to tak nie wygląda.
Zajmuje się wynalazkami. To są takie rozwiązania np. techniczne, których świat nie zna a uczeni mogą się z nimi zapoznać dopiero przez lekturę stosownej publikacji.
Oczywiście, że w mojej pracy korzystam z wiedzy wielu innych ludzi. Pracując nad innowacją muszę znać /poznać obecny stan techniki aby znane rozwiązanie ulepszyć lub stworzyć coś nowego. Zgłoszone rozwiązanie jest weryfikowane przez urzędy patentowe prawie na całym świecie i musi się jeszcze dać zastosować przemysłowo.
Zatem, informacja, szczegółowa wiedza i znajomość tematu jest niezbędna. i nie mogę sobie pozwolić na fantazje jak w twoim wydaniu. Piszę to nie jako krytyka artykułu , bardziej jako protest w obronie tych którzy je czytają będą czytać i utrwali im się nie prawdziwa wiedza z opłakanym skutkiem jakby chcieli ją wykorzystać i zastosować w praktyce. Na 1000 najlepszych uczelni na świecie, 10 zajmują Polskie, najlepsza 400 miejsce. Może stan wiedzy o tym decyduje? Niektórzy publicyści nie mają oporu pisać wprost-np. nauka nie zna jeszcze dokładnego działania a próbując przybliżyć dane zjawisko ludziom, nie wciskają kitu. Polecam naśladownictwo. Nasza młodzież jest dość kumata i przy prawidłowej wiedzy szybko przestanie mówić, że prąd jest i bierze się z gniazdka. Chyba ze komuś bardzo zależy aby dalej istniało określenie Ciemny Lud
Rozumiem. Każdy ma jakieś swoje oczekiwania i wyobrażenie na temat idealnej metody nauczania. Nie dziwi mnie również, że dla kogoś, kto zajmuje się wynalazkami, prezentowany tutaj poziom może być niewystarczający. To po prostu nie ten adres.
Sprostuję jednak dwie rzeczy:
1. W artykule jasno napisałem, że prezentowane zagadnienia są uproszczeniem i prąd w rzeczywistości tak nie płynie. Ale skoro i tak nie wiemy jak płynie, to takie wyobrażenie jest dobre jak każde inne. A to dlatego, że prowadzi do tego samego wyniku (w skali makro zjawiska kwantowe się załamują i i tak nie mają żadnego znaczenia). Zresztą w wielu moich artykułach piszę o tym jak wielu rzeczy nie wiemy. Staram się przy tym nie zostawiać czytelnika z suchym wzorem i dać mu jakiś punkt zaczepienia, pozwalający lepiej zapamiętać temat. Też kiedyś poczułem się oszukany, gdy nauczyciel w szkole średniej zdradził mi, że równanie kwadratowe, którego delta jest mniejsza od zera również ma rozwiązania. Ale czy powinniśmy w takim razie wprowadzać liczby zespolone i rachunek różniczkowy od najmłodszych lat? Wtedy bylibyśmy absolutnie szczerzy i trzymali się aktualnej wiedzy, a nie tej z XIV wieku. Według mnie nie tędy droga. Stopniowanie wiedzy to jest moje podejście, dlatego w moich bardziej zaawansowanych artykułach przeczytasz o nieco innym spojrzeniu na ruch ładunków elektrycznych.
2. Pisząc artykuły opieram się nie tylko na polskich publikacjach, ale też bardzo wielu zagranicznych. Nie studiowałem co prawda na MIT ani na Yale, ale teksty wychodzące spod pióra absolwentów tych uczelni nie różnią się od tych wydawanych u nas. To samo z wykładami dostępnymi choćby na Youtube. Więc albo elektrotechniki uczy się wszędzie tak samo, albo ja nie potrafię znaleźć tych lepszych publicystów. Skoro wspomniałeś o takowych, to może podrzucisz jakieś tytuły? Sam przez cały czas się uczę i bardzo chętnie poznam nowoczesne metody nauczania elektrotechniki.
Głupio przyznać, ale w zasadzie jestem elektrykiem po technikum. Niestety życie i różne problemy tak mi się potoczyły, że nie pracowałem w zawodzie, a przedmioty zawodowe średnio mi szły.Dopiero teraz po kilku latach chcę zacząć od nowa przygodę z elektryką 😀 Super, że odpowiadasz na pytania, wahałem się, czy pytać o taki banał, mam uraz po technikum, gdzie nauczyciele oburzali się i prawie wyśmiewali za takie pytania, ale co poradzić taki jest w tym kraju poziom w szkolnictwie, sama wiedza to za mało, żeby uczyć, myślę że ty to robisz odpowiednio 😀
Sam to przerabiałem na studiach! W Polsce niestety panuje jakaś taka dziwna relacja, że jak ktoś coś wie, to się ma za nie wiadomo kogo i do osób, które zadają absolutnie podstawowe pytania, odnosi się jak do głupców. Stąd wyrobiliśmy sobie słuszny strach przed zadawaniem pytań w ogóle.
Mnie o absolutne podstawy pytają zarówno nastolatkowie jak i osoby po 60stce i nie widzę w tym problemu. Być może ja za 30 lat też zainteresuję się na przykład medycyną i będę chciał ogarnąć kilka podstaw. Czy mam się wtedy bać pytać?
Wspomniałeś o technikum. Wszyscy wiemy jaki jest poziom szkół średnich w Polsce. Idąc do technikum elektrycznego nie należy zakładać, że można po nim zostać elektrykiem. Połowa problemu to sam system edukacji. Druga połowa to fakt, że w klasie są zwykle 1-3 osoby, które faktycznie przyszły się czegoś nauczyć i kilkanaście innych, które są, bo muszą. Na szczęście żyjemy w takich pięknych czasach, że szkoła to nie jedyne miejsce, w którym można zdobywać wiedzę.
Pozdrawiam!
Czy w takim razie wszystkie elementy ochronne na prąd robi się z teflonu? Jak to jest np. Z probówką,rękawicami i sondami miernika? Czy zwykły śrubokręt można przyłożyć do 230 V? Co do pracy którą wykonujesz doskonała robota, myślę że super byłoby, gdyby każdy uczeń technikum elektrycznego już na 1 roku, dostał do wyuczenia wszystkie twoje artykuły. Dałoby to niezbędne ogólne pojęcie i byłoby już dużo łatwiej się uczyć. Niestety ja nie miałem takiego przywileju i było ciężko, cały czas czułem braki i wielu rzeczy nie ogarniałem.
Z teflonu, lateksu i wielu różnych mieszanek polimerów. Rezystywność to nie jedyny parametr, stąd zależnie od potrzeb materiały są przeróżne. Co do obudowy probówki i sond miernika to nie wiem dokładnie jakie stosuje się materiały (zapewne różne, w zależności od producenta), w każdym razie przy zakupie warto sprawdzić przed jakim maksymalnym napięciem chronią nas takie sondy.
I o ile sond czy probówek raczej nie używa się w przy innych pracach (są to typowe narzędzia elektryczne), o tyle z wkrętakami jest już inna historia. Wkrętak wkrętakowi nierówny. Większość z nich ma na tyle grubą izolację, że raczej nic Ci się nie stanie, ale z drugiej strony rynek jest pełen chińskiej tanizny i nie warto ryzykować. Dlatego też każda szanująca się firma posiada linię specjalnych narzędzi ręcznych dla elektryków, z tzw. izolacją VDE, a konkretniej izolacją z certyfikatem VDE. Co to jest? Najlepiej objaśnia to ten artykuł: https://toya24.pl/Narzedzia-VDE-Przydatne-informacje-clinks-pol-87.html
Reasumując – jeśli ktoś nie jest elektrykiem nie polecam do gniazdka wkładać niczego, co nie jest wtyczką jakiegoś znanego nam urządzenia. Jest takie słynne powiedzenie, że saper myli się tylko raz. Z elektrykami-amatorami jest podobnie.
Przeczytałem większość Twoich artykułów .
Dały mi one obraz tego czym jest prąd.
Sporo kwestii zrozumiałem ale jest jedna której zrozumieć dalej nie mogę.
Zacznę po kolei.
Jak wiemy prąd to uporządkowany ruch ładunkówów elektrycznych. Przepływają one przez przekrój poprzeczny przewodnika pod pływem przyłożonego napięcia. Napięcie określa ile energii przypada na każdy kulomb ładunku. Jeśli to podzielimy to mówi nam też ile energii przypada na każdy elektron.
Bo jeden kulomb to około 6 trylionów elektronów. Więc można się też dowiedzieć ile przypada na dany elektron. Oczywiście jednostki byłyby małe i nie wygodne dlatego rozpatrujemy to w kontekście większego kulomba.
Rezystancja mówi nam jak ciężko elektronowi jest przedrzeć się przez dany rezystor .
W artykule o spadku napięcia znajduje się animacja. Żarnik przedstawiony jest jako opornik w którym elektrony zderzają się z jego atomami i w ten sposób energia pędzącego elektronu zamieniana jest na ciepło. Prędkość pędzącego elektronu opisuje natężenie prądu czyli stosunek ilości ładunku do czasu jego przepływu. Im szybciej pędzi elektron tym więcej ma on energii i mocniej uderza w atom opornika. Możemy wiec wnioskować ze ilość oddawanej energii na rezystorze zależy od prędkości elektronu i budowy opornika. Im większa rezystancja tym bardziej upakowane atomy i zderzeń jest więcej. Jak wiadomo każde zderzenie to ileś oddanej energii. Pisze oczywiście o energii oddawanej przez pojedynczy elektron. Czym innym jest moc czyli P=UxI .Tutaj znaczenie ma łączna ilość energii oddawanej przez wszystkie elektrony. Wróćmy jeszcze na chwile do natężenia prądu.
W jednym komentarzu napisałeś mi ,że albo mamy większe natężenie jeśli elektrony płyną szybciej albo większe jeśli płynie ich więcej obok siebie np. większa średnica przewodnika .
Teraz rozpatrzmy taki przypadek mamy obwód . Składa się on z baterii 5 V i rezystora , oczywiście też przewodów (ich rezystancje na razie pomińmy). Elektrony płyną aby wyrównać potencjał siła i ilość zderzeń w oporniku jest taka aby elektron oddał swą zgromadzoną energie. Jeśli zwiększymy napięcie to ilość zderzeń w oporniku zostanie taka sama ale elektron popłynie szybciej (bo natężenie wzrośnie ) dlatego siła zderzenia będzie większa. W sumie przy tej samej liczbie zderzeń ale mocniejszych zostanie oddana większa energia. Wszystko się zgadza. Jeśli byśmy zaś napięcie zmniejszyli to ilość zderzeń zostanie taka sama ale będą słabsze (natężenie spadnie ) czyli mniej energii odda każdy elektron .Jeśli np. zwiększymy rezystancje opornika to z kolei zderzeń będzie więcej ale będą słabsze i znowu elektron przepływając przez rezystor odda odpowiednia ilość nagromadzonej przez siebie energii.
Teraz załóżmy ze mamy rezystory połączone równolegle. Napięcie zasilania wynosi 5 v jeden rezystor jest mniejszy a drugi większy. Oba maja takie same napięcia jak to możliwe. Wydaje mi się że tak: na większym rezystorze zderzeń jest więcej (większa rezystancja) ale elektron uderza słabiej(mniejsze natężenie). Na mniejszym zderzeń jest mniej(mniejsza rezystancja) ale elektron uderza mocniej (większe natężenie). W efekcie ilość wytracanej energii na jednym i drugim rezystorze może być taka sama .I teraz wreszcie sprawa której nie rozumiem. Bo nawiązując do tego co pisałeś wcześniej. Jeśli natężenie jest większe to albo elektrony płynna szybciej albo elektronów płynie więcej obok siebie w jednostce czasu.
I teraz wersja druga – elektronów płynie więcej obok siebie (większa średnica opornika) ale ich prędkość jest taka sama. Czyli natężenie wzrosło nie dla tego ze elektrony płyną szybciej tylko płynie ich więcej .
Ponownie taki sam obwód takie same oporniki jeden o większej rezystancji drugi o mniejszej.
Jeśli tak by się działo to siła zderzeń przypadająca na każdy elektron byłaby taka sama na jednym i drugim rezystorze. Dlatego że na jednym i drugim rezystorze pojedynczy elektron pędzi z tą samą prędkością. W dodatku na jednym zderzeń było by więcej a na drugim mniej (różne rezystancje). Wiec wychodziło by na to ze pojedynczy elektron energii na jednym rezystorze wytraca więcej a na drugim mniej. Wówczas napięcia nie mogą być takie same . Właśnie to chce zrozumieć jak to się ma do logiki zderzeń z atomami rezystora. Wiem ze jest prawo Kirkofa ze skoro każdy elektron dostaje tyle samo energii od baterii a potem trafia albo na jeden albo na drugi rezystor w polaczeniu równoległym to musi ją całą oddać dlatego napięcia są takie same. Jednak jak to wygląda od strony teorii zderzeń?
No chyba że – elektronów płynie więcej obok siebie ale ich prędkości na poszczególnych opornikach też są różne. Bo to by miało sens .
Napisałeś tak długi komentarz, że musiałbym odpowiedzieć na niego jeszcze dłuższą wypowiedzią. Dlatego postanowiłem, że napiszę do Ciebie maila i tam rozwikłamy wszystko krok po kroku 🙂
Super dzięki wielkie czekam
Czy jest szansa abym dostal na maila kopie odpowiedzi na pytanie urzytkownika „Amadeusz” ?
Nie jest to niestety możliwe, gdyż zrobiła nam z się wówczas z tego długa rozmowa na kilkanaście maili (postanowiłem omówić temat krok po kroku). Za to bardzo chętnie odpowiem na Twoje pytania, czy to tutaj w komentarzach, czy mailowo.
Świetny artykuł, przez animacje i wizualizacje jest o wiele łatwiej zrozumieć temat! Co do pierwszego przykładu, że rezystancja jest proporcjonalna z długością przewodnika nie mam żadnych wątpliwości, tak jak w artykule: elektrony doświadczają większej ilości zderzeń i na ich skutek tracą część swojej energii, dwa razy dłuższa droga, dwa razy więcej zderzeń. Jednak 'balans’ nie zgadza mi się w drugim przykładzie… Tak jak Pan opisał w sytuacji a) mamy w sumie 10 pojedynczych strat energii i dotrą 2 elektrony w ciągu 1 sekundy, za to w przykładzie b) mamy 20 pojedynczych strat energii i dotrą 4 elektrony w ciągu 1 sekundy. I tak jak Pan napisał w artykule: elektronów dotarło 2 razy więcej w ciągu 1 sekundy… ale przecież też straciły 2 razy więcej pojedynczych energii, więc z tego by wynikało że oba te czynniki mogłyby się w jakiś sposób 'wykasować’. Wiedząc, że w rzeczywistości te dwa czynniki się nie kasują, wiem że ten 'balans’ nie może zachodzić, więc bym był bardzo wdzięczny jeżeli mógłby Pan wskazać lukę w moim rozumowaniu 🙂
Owszem, drugi przykład wygląda dość kontrowersyjnie, głównie przez to, że próbuje bazować na tym pierwszym. Jego zamysł jest jednak trochę inny. Załóżmy, że na starcie każdy elektron ma 10 J energii, a każde zderzenie kosztuje go 1 J. W przypadku a) dwa elektrony dowiozą do mety 10 J energii (bo każdy straci po 5). W przypadku b) elektrony dowiozą 20 J energii (każdy również traci po 5 J, ale elektrony są 4).
Dzięki za zwrócenie uwagi na tę niejasność. Poprawię ten akapit tak, by był bardziej zrozumiały.
Robert,
Wybacz Dawidzie że kopiują Twoją wypowiedz, ale w 100% się z Tobą zgadzam.
Zafascynował mnie wszystkie Pana Artura artykuły z teorii Elektryki…a zaczęło od lekcji gry na gitarze, które Pan Artur prowadził.
Pozdrawiam
W swoim życiu nie spotkałem się z żadną książką /artykułem, który by w tak przejrzysty i jakże przyjemny sposób przedstawiał i rozkładał na części pierwsze prawa rządzące się prądem. Życzyłbym każdemu uczniowi w naszym kraju, żeby w swoim życiu spotykał samych takich nauczycieli, którzy umieliby tak jak Pan z pasją i rzetelnością przekazywać wiedzę. Mam nadzieję, że Pan się dopiero rozpędza z tymi artykułami. Gorąco pozdrawiam
Rezystywność w tabelce jest uproszczoną jednostką. Do przeliczeń jest to Ohm * metr kwadratowy (przekroju) / metr długości w uproszczeniu Ohm * metr. Dla drutu o przekroju w mm kwadratowych należy zamienić wartość przekroju z metra kwadratowego na mm kwadratowy.
Bardzo fajny artykuł, pomógł mi zrozumieć różnicę między rezystywnością, a rezystancją. Jedyna drobna uwaga – przy użyciu wzorów byłby mile widziane legendy do poszczególnych oznaczeń wraz z używanymi jednostkami.
Pozdrawiam!
Kiedyś podłączyłem pod przedłużacz za 5 zł z targu suszarkę i i grzałkę(próbowałem coś szybko ogrzać) XD.
Przedłużacz tylko zaskwierczał i chyba wybiło korki. Okazało się, że przewody były bardzo cienkie, wręcz nitki, rozpoznałem to jako przyczynę, ale nie rozumiałem do końca.
Ten artykuł wszystko wyjaśnia : nie było miejsca dla Ciebie elektronie 🙂
Bardzo przejrzysty artykuł, dobrze skomponowany. W dzisiejszych czasach często jest trudno wytłumaczyć jakieś prawo czy metodę pomiaru, a nawet wiadomości elementarne jak np: prąd elektryczny. Artykuł z chęcią przyciągnał moją uwagę i będę częściej z nich korzystał.
Dziękuję bardzo za przekazaną wiedzę, żeby tak profesorowie na uniwersytetach tłumaczyli i przedstawiali, to nauka była by czystą przyjemnością i radością, Mam nadzieję że to nie koniec artykułów tego typu, są one bardzo pomocne, pomagają zdobyć nową wiedzę i ugruntować starą. Pozdrawiam serdecznie !
Cała przyjemność po mojej stronie! Artykuły pojawiają się i będą pojawiać dalej, więc zapraszam ponownie!
Rewelacja pod każdym względem,podziękowanie dla Autora.
W swoim życiu nie spotkałem się z żadną książką /artykułem, który by w tak przejrzysty i jakże przyjemny sposób przedstawiał i rozkładał na części pierwsze prawa rządzące się prądem. Życzyłbym każdemu uczniowi w naszym kraju, żeby w swoim życiu spotykał samych takich nauczycieli, którzy umieliby tak jak Pan z pasją i rzetelnością przekazywać wiedzę. Mam nadzieję, że Pan się dopiero rozpędza z tymi artykułami. Gorąco pozdrawiam